Implementation of FASILL in FLOPER
During the last years we have developed the FLOPER tool, initially intended for manipulating MALP programs6. In its current development state, FLOPER has been equipped with new features in order to cope with more expressive languages and, in particular, with FASILL (that is freely accessible in its url http://dectau.uclm.es/floper/?q=sim where it is possible to test/download the new prototype incorporating the management of similarity relations. In this section we briefly describe the main features of this tool before presenting the novelties introduced in this work.
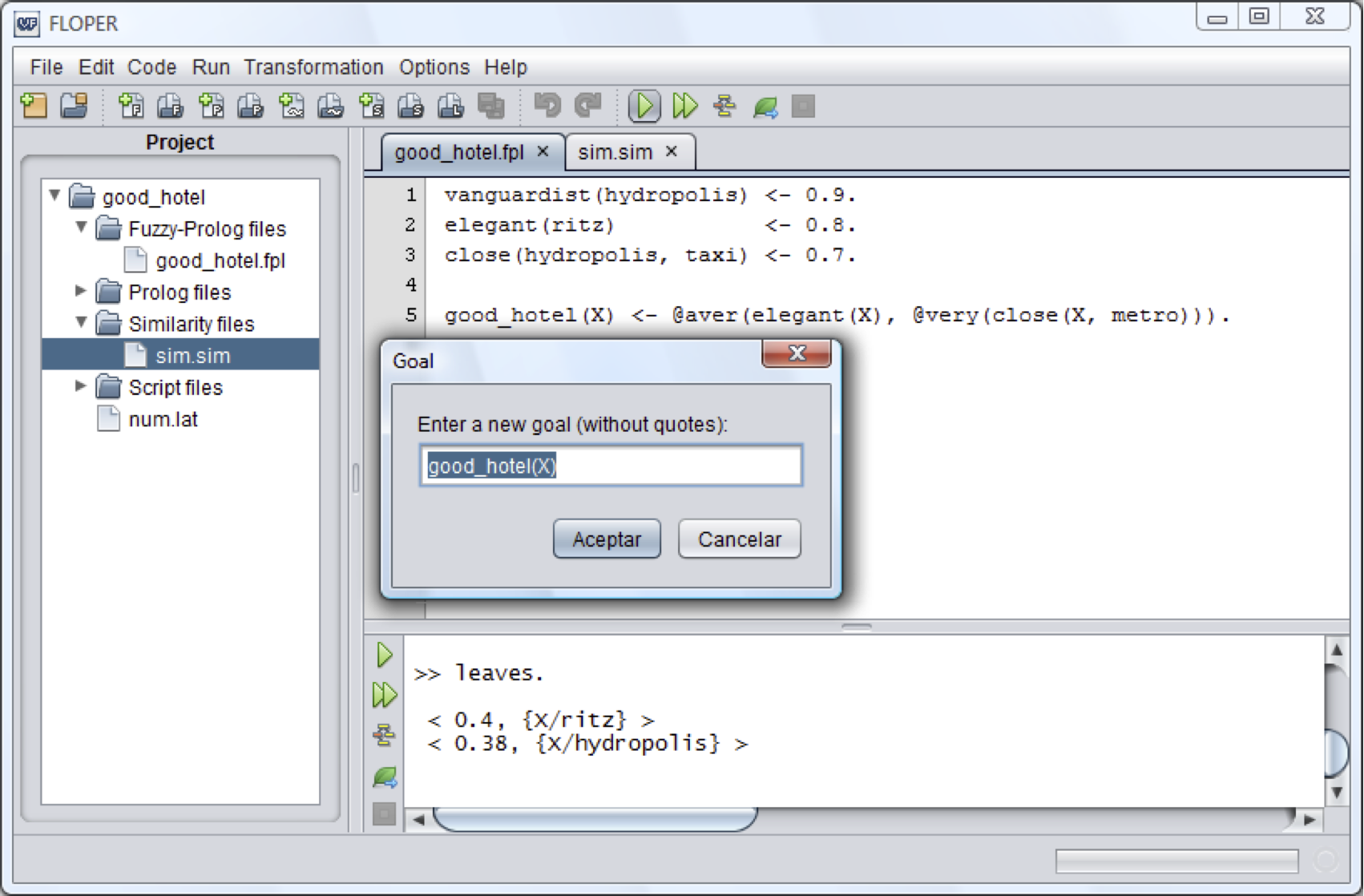
Figure 2: Screen-shot of a work session with FLOPER managing a FASILL program
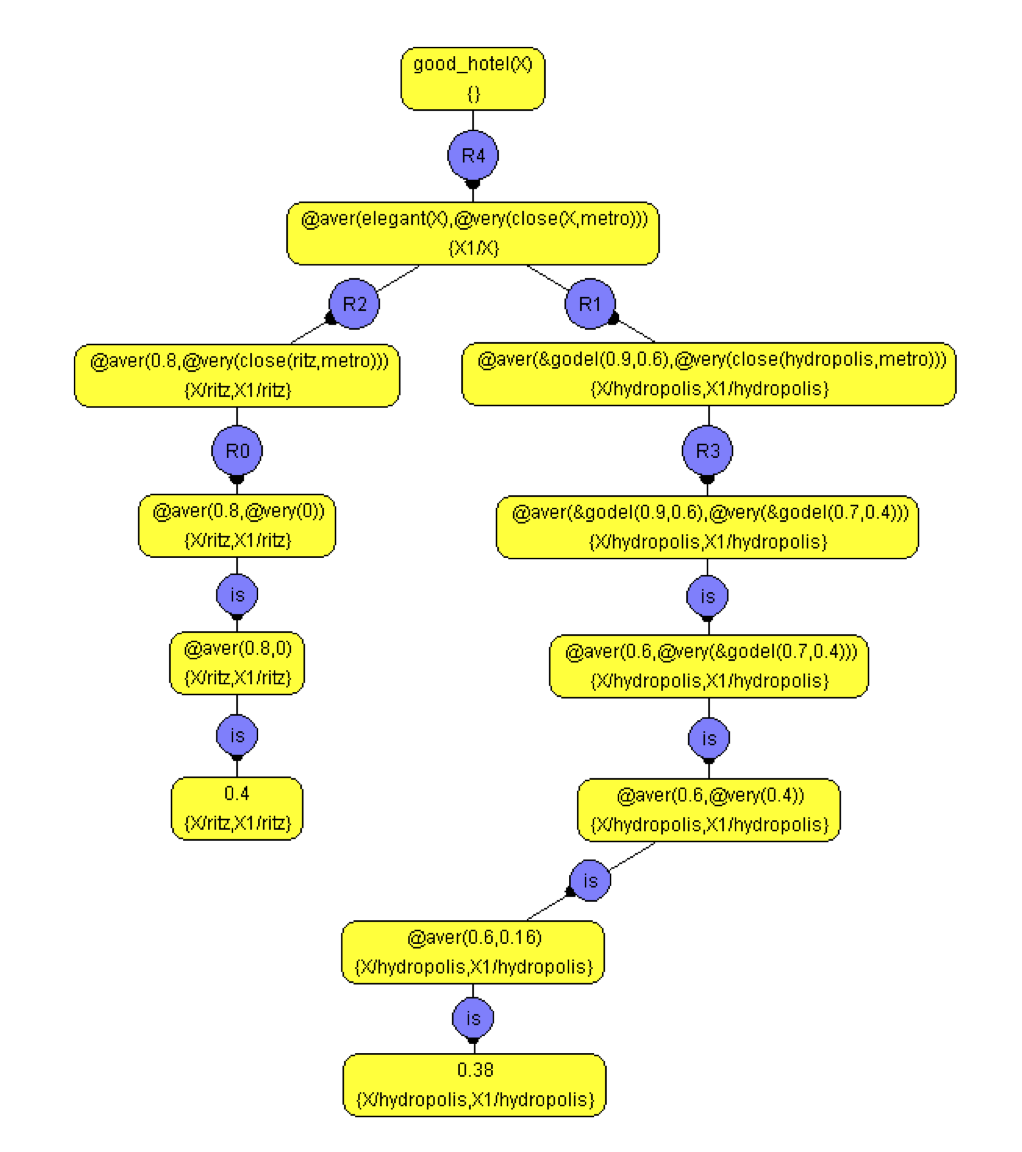
Figure 3: An execution tree as shown by the FLOPER system
FLOPER has been implemented in Sicstus Prolog v.3.12.5 (rounding about 1083 lines of code, where our last update supposes approximately a 30% of the final code) and it has been recently equipped with a graphical interface written in Java (circa 2000 lines of code). More detailed, the FLOPER system consists in a ”.jar” java program that runs the graphical interface. This ”.jar” program calls a ”.pl” file containing the two main independent blocks: 1) the Parsing block parses FASILL files into two kinds of prolog code (a high level platform-independent Prolog program and a set of facts to be used by FLOPER), and 2) the Procedural block performs the evaluation of a goal against the program, imple- menting the procedural semantics previously described. This code is completed with a configuration file indicating the location of the Prolog interpreter as well as some other data.
When the graphical interface is executed, it offers a menu with a set of commands grouped in four submenus:
- “Program Menu”: includes options for parsing a FASILL program from a file with extension “.fpl”, saving the generated PROLOG code to a “.pl” file, loading/parsing a pure PROLOG program, listing the rules of the parsed program and cleaning the database.
- “Lattice Menu”: allows the user to change and show the lattice (implemented in PROLOG) associ- ated to a fuzzy program through options lat and show, respectively.
- “Similarity Menu”: option sim allows the user to load a similarity file (with extension “.sim”, and whose syntax is detailed further in the Similarity Module subsection ) and tnorm sets the conjunction to be used in the transitive closure of the relation.
- “Goal Menu”: by choosing option intro the user introduces the goal to be evaluated. Option tree draws the execution tree for that goal whereas leaves only shows the set of fuzzy computed answer contained on it, and depth is used for fixing its maximum depth.
The lattice module. Lattices are described in a .lat file using a language that is a subset of PROLOG where the definition of some predicates are mandatory, and the definition of aggregations follows a certain syntax. The mandatory predicates are member/1, that identifies the elements of the lattice, bot/1 and top/1, that stand for the infimum and supremum elements of the lattice, and leq/2, that implements the ordering relation. Predicate members/1, that returns in a list all the elements of the lattice, is only required if it is finite. Connectives are defined as predicates whose meaning is given by a number of clauses. The name of the predicate has the form and label, or label or agr label whether it implements a conjunction, a disjunction or an aggregator, where label is an identifier of that particular connective (this way one can define several conjunctions, disjunctions and other kind of aggregators instead of only one). The arity of the predicate is n + 1, where n is the arity of the connective that it implements, so its last parameter is a variable to be unified with the value resulting of its evaluation.
Example 1. For instance, the following clauses show the PROLOG program modeling the lattice of the real interval [0,1] with the usual ordering relation and connectives (conjunction and disjunction of the Product logic, as well as the average aggregator):
member(X):- number(X), 0=<X, X=<1.
and_prod(X,Y,Z) :- Z is X*Y.
or_prod(X,Y,Z) :- U1 is X*Y, U2 is X+Y, Z is U2-U1.
agr_aver(X,Y,Z) :- U1 is X+Y, Z is U1/2.
leq(X,Y):- X=<Y.
bot(0).
top(1).
The similarity module. We describe now the main novelty performed in the tool, that is the ability to take into account a similarity relation. The similarity relation R is loaded from a file with extension .sim through option sim. The relation is represented following a concrete syntax:
⟨Relation⟩ ::= ⟨Sim⟩ ⟨Relation⟩ | ⟨Sim⟩
⟨Sim⟩ ::= ⟨Idf ⟩[‘/’ ⟨Intn⟩] ‘∼’ ⟨Idg⟩[‘/’ ⟨Intn⟩] ‘=’ ⟨r⟩ ‘.’ | ‘∼’ ‘tnorm’ ‘=’ ⟨tnorm⟩
The Sim option parses expressions like “ f ∼ g = r”, where f and g are propositional variables or con- stants and r is an element of L. It also copes with expressions including arities, like “ f /n ∼ g/n = r” (then, f and g are function or predicate symbols). In this case, both arities have to be the same. It is also possible to explicit, through a line like “∼ tnorm = ⟨label⟩” the conjunction to be used further in the construction of the transitive closure of the relation. Internally FLOPER stores each relation as a fact r in an ad hoc module sim as r(f/n,g/n,r), where n = 0 if it has not been specified (that is, the symbol is considered as a constant). The .sim file contains only a small set of similarity equations that FLOPER completes by performing the reflexive, symmetric and transitive closure. The first one simply consists of the assertion of the fact r(A,A,⊤). The symmetric closure produces, for each r(a,b,r), the assertion of its symmetric entry r(b, a, r) if there is not already some r(b, a, r′ ) where r ≤ r′ (in this case r(a, b, r) will be rewritten as r(a, b, r′ ) when considering r(b, a, r)). The transitive closure is computed by the next algorithm7, where ∧ stands for the conjunction specified by the directive “tnorm”, and “assert” and “retract” are self-explainable and defined as in PROLOG:
Transitive Closure
forall r(A,B,r1) in sim
-
forall r(B,C,r2) in sim
- r = r1 ∧ r2
-
-
if r(A,C,r′) in sim and r′ < r
- retract r(A,C,r′) from sim
- retract r(C,A,r′) from sim
- end if
-
if r(A,C,r′) not in sim
- assert r(A,C,r) in sim
- assert r(C,A,r) in sim
- end if
-
if r(A,C,r′) in sim and r′ < r
- end forall
end forall
It is important to note that, it is not relevant if the user provides (apparently) inconsistent similarity equations, since FLOPER automatically changes the user values by the appropriate approximation degrees in order to preserve the properties of a similarity. For instance, if a user provides a set of equations such as, a∼b=0.8, b∼c=0.6 and a∼c=0.3, after the application of our algorithm for the con- struction of a similarity, results in the set of equations a ∼ b = 0.8, b ∼ c = 0.6 and a ∼ c = 0.6, which positively preserves the transitive property8.
Example 2. In order to illustrate the enhanced expressiveness of FASILL, consider the program ⟨Π,R,L⟩ (where L is the real interval [0, 1] and ≤ is the usual ordering relation on real numbers), that models the concept of good hotel, that is, an elegant hotel that is very close to a metro entrance, as seen in Figure 2. Here, we use an average aggregator defined as @ ̇ avg (x, y) = (x + y)/2, whereas very is a linguistic modifier implemented as well as an aggregator (with arity 1) with truth function @ ̇ very x = x2. The sim- ilarity relation R states that elegant is similar to vanguardist, and metro to bus and (by transitivity) to taxi:
~tnorm = godel
metro ~ bus = 0.5.
elegant/1 ~ vanguardist/1 = 0.6.
bus ~ taxi = 0.4.
We also state that the t-norm to be used in the transitive closure is the conjunction of Go ̈del (i.e., the infimum between two elements). With respect to this program (the set of rules from Figure 2, the lat- tice [0,1] with the usual ordering relation and the similarity relation just described before), the goal good hotel(X) produces two fuzzy computed answers: <0.4, X/ritz> and <0.38, X/hydropolis>. Each one corresponds to the leaves of the tree9 depicted in Figure 2. Note that for reaching these solu- tions, a failure step was performed in the derivation of the left-most branch, whereas in the right-most one (and this is the crucial novelty w.r.t. previous versions of the FLOPER tool) there exist two success- ful steps exploiting the similarity relation which firstly relates elegant and vanguardist and secondly (by transitivity) metro and taxi when solving atom close(hydropolis,metro), which illustrates the flex- ibility of our system.
Ending this section, it is worthy to say that our approach differs from the one presented in [1] since they employ a combination of transformation techniques to first extract the definition of a predicate “∼”, simulating weak unification in terms of a set of complex program rules that extends the original program. Finally, this predicate “∼” is reduced to a built-in proximity/similarity unification operator (in this case not implemented by rules and very close to the implementation of our weak unification algorithm) that highly improves the efficiency of their previos programming systems.
6 The MALP language is nowadays fully subsumed by the new FASILL language just introduced in this web, since, given a FASILL program P = ⟨Π,R,L⟩, if R is the identity relation (that is, the one where each element of a signature Σ is only similar to itself, with the maximum similarity degree) and L is a complete lattice also containing adjoint pairs [8], then P is a MALP program too.
7 It is important to note that this algorithm must be executed right after performing the symmetric, reflexive closure.
8 For simplicity we have omitted the equations obtained during the construction of the reflexive, symmetric closure.
9Each state contains its corresponding goal and substitution components and they are drawn inside yellow ovals. Compu- tational steps, colored in blue, are labeled with the program rule they exploit in the case of successful steps or the annotation “R0” in the case of failure steps (observe that, “R0” is a simple notation and do not correspond with any existing rule). Finally, the blue circles annotated with the word “is”, correspond to interpretive steps.