Our parser has been implemented by using the classical DCG's (Definite Clause Grammars) resource of the Prolog language, since it is a convenient notation for expressing grammar rules. At the end of this section we show an example of a possible work sesion 's trace. The application contains about 300 clauses and once it is loaded inside a Prolog interpreter (in our case, Sicstus Prolog), it shows a menu which includes (among other ones) options for:

Figure 1: Floper Menú.

• Loading a prolog file with extension .pl. This action is useful for reading a file containing a set of Prolog clauses implementing aggregators, user predicates, etc. Nevertheless, the original connectives of the Product, Gödel and Lukasiewicz logic, expressed in the Prolog style seen in the previous section, are defined in file prelude.pl, which is automatically loaded by the system at the beginning of each work session.
• Parsing a fuzzy program included in a file with extension .fpl. In order to simultaneously perform the parsing process with the code generation, each parsing predicate used in DCG's rules, has been augmented with a variable as extra argument which is intended to contain the Prolog code generated after parsing the corresponding fragment of fuzzy code. We also admit the presence of pure Prolog clauses inside a .fpl file, by preceding them with a $ symbol.
• Listing the set of Prolog clauses loaded from a .pl file as well as those ones obtained after compiling an .fpl. Of course, the original fuzzy program contained in this last file is also displayed.
• Saving the resulting Prolog code into a file. Here we want to point out that the set of clauses obtained during the compilation process is also automatically asserted in the data base of the Prolog interpreter, which obviously also contains the clauses implementing the proper tool. This action helps the development of the following option.
• Executing a fuzzy goal after being introduced from the keyboard. As we have seen in the previous section, if the goal provided by the user is p(X) &godel r(a), then the system translates it into the standard Prolog goal: (X,_TV1),r(a,_TV2),and_godel(_TV1,_TV2,_TV3).

However, this expression needs a final manipulation before being executed, which consists in renaming its last truth variable (in this case _TV3) by Truth_degree. Now, note that the set of non anonymous variables in the resulting Prolog goal, are simply those ones belonging to the original fuzzy goal (i.e., X) and the one containing its associated truth degree (i.e., Truth_degree). Then, after re-evaluating the Prolog goal

?- p(X,_TV1),r(a,_TV2),and_godel(_TV1,_TV2,Truth_degree).

the Prolog interpreter returns the following pair of desired fuzzy computed answers:

X=a, With_Truth_Degree=0.48; X=b, With_Truth_Degree=0.31999; no

The previous set of options suffices for executing fuzzy programs: all internal computations (including compiling and executing) are pure Prolog derivations whereas inputs (fuzzy programs and goals) and outputs (fuzzy computed answers) have always a fuzzy taste, which produces the illusion on the user of being working with a purely fuzzy tool. However, when trying to go beyond program execution, our method becomes insufficient. In particular, observe that we can only simulate complete fuzzy derivations (by performing the corresponding Prolog derivations based on SLD-resolution) but we can not generate partial derivations or even apply a single admissible/interpretive step on a given fuzzy expression. This kind of low-level manipulations are mandatory when trying to incorporate to the tool some program transformation techniques such as those based on fold/unfold or partial evaluation we have described in [7, 8].

To achieve this aim, we have conceived a new low-level representation for the fuzzy code: each parsing predicate used in DCG's rules (which already contains a parameter allocating the Prolog code obtained after the compilation process) has also been augmented with a second extra argument for storing now the new representation associated to the corresponding fragment of parsed fuzzy code. For instance, after parsing the first rule of our program, we obtain the following expression (whose components have obvious meanings):

      rule( number(1),
            head(atom(pred(p,1),var('X')])),
            impl(prod),
            body(and(godel,2,[atom(pred(q,2),[var('X'),var('Y')]),
                              atom(pred(r,1),[var('Y')])])),
            td(0.8)).

Once obtained at compilation time, this term is asserted into the database of the Prolog interpreter as a Prolog fact, thus making accessible this low-level representation of the fuzzy rule to the whole application. Two more examples: substitutions are modeled by lists of terms of the form link(V, T) where V and T contains the code associated to an original variable and its corresponding (linked) fuzzy term, respectively, whereas an state is represented by a term with functor state/2. We have implemented predicates for manipulating such kind of code at a very low level in order to unify expressions, compose substitutions, apply admisible/interpretive steps, etc.

With this nice representation, we can also build execution trees with any level of depth, thus producing terms of the the form tree(S, L), where S represents the state rooting the tree, and L is the list containing its set of children trees. From here, we are just implementing all the transformation techniques we have proposed in the past: the key point is the correct manipulation of the leaves of this kind of partially evaluated trees, in order to produce unfolded/folded rules, partially evaluated programs, and so on. These actions, together with the study of mechanism for surpassing the simpler case of modeling truth degrees with real numbers, are some high-priority tasks in our group for updating the FLOPER system.

Figure 2: Example of execution option 'tree'.

Work sesion 's trace.

Now we show a basic work sesion's trace step by step. The idea is loading program 'example1.fpl' (in folder 'C:/FLOPER/examples/example1.fpl') and then introducing and executing a goal, in order to finally display the associated execution tree. Code of 'example1.fpl' is the same as code that we use in examples 1.3 and 2.3 of 'Procedural Semantic' of section 'Fuzzy Logic Programs'.

• Step 1. Load file 'floper.pl' using option 'consult' of Sictus Prolog:

Figure 3: Option 'Consult' of Sictus Prolog

            So we load the tool (see Figure 1 of this section, FLOPER's main menu).

• Step 2. Now we proceed to parse, translate and load the fuzzy code included in file 'example1.fpl' through option 'parse' (the file's path must be written between quotes):

Figure 4. Option 'parse'.

Remember you can see the original fuzzy code as well as the generated pure Prolog code by using option 'list':

Figure 5. Option 'list'.

• Step 3. For introducing goal 'p(X)' we use option 'intro' (goal must be written between quotes):

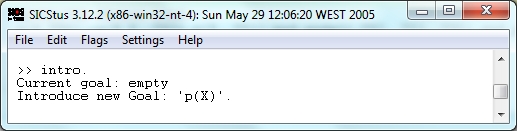
Figure 6. Option 'intro'.

• Step 4. Now, for executing the previous goal against the parsed program 'example1.fpl', we simply invoke option 'run':

Figure 7. Option 'run'.

• Step 5. To display the partial execution of the program, we can first select how to display the steps of the interpretive phase of the resolution using option 'ismode'. There are three options: l (large) shows only the result of the interpretive phase; m (medium) shows each interpretive step; and s (small) shows small interpretive steps:

Figure 8. Option 'ismode'.

• Step 6. To display the partial execution tree associated to the program and goal above, we use option 'tree':

Figure 9. Option 'tree' with 'ismode' set to 's' (small).

Figure 10. Option 'tree' with 'ismode' set to 'm' (medium).

Figure 11. Option 'tree' with 'ismode' set to 'l' (large).

Remember you can change tree's depth via option 'depth'.

Finally, FLOPER also includes other typical options for saving, quiting, clearing and so on.