We have recently conceived a very easy way to model truth degrees lattices for being included into the FLOPER tool. All relevant components of each lattice can be encapsulated inside a Prolog file which must necessarily contain the definitions of a minimal set of predicates defining the set of valid elements (including special mentions to the "top" and "bottom" ones), the full or partial ordering established among them, as well as the repertoire of fuzzy connectives which can be used for their subsequent manipulation. In order to simplify our explanation, assume that file "bool.pl" refers to the simplest notion of (a binary) adjoint lattice, thus implementing the following set of predicates:

• member/1 which is satisfied when being called with a parameter representing a valid truth degree. In the case of finite lattices, it is also recommend to implement members/1 which returns in one go a list containing the whole set of truth degrees. For instance, in the boolean case, both predicates can be simply modeled by the Prolog facts: member(0)., member(1). and members([0,1]).
• bot/1 and top/1 obviously answer with the top and bottom element of the lattice, respectively. Both are implemented into "bool.pl" as bot(0). and top(1).
• leq/2 models the ordering relation among all the possible pairs of truth degrees, and obviously it is only satisfied when it is invoked with two elements verifying that the first parameter is equal or smaller than the second one. So, in our example it suffices with including into "bool.pl" the facts: leq(0,X). and leq(X,1).
• Finally, given some fuzzy connectives of the form &_label1 (conjunction), ∨_label2 (disjunction) or @_label3 (aggregation) with arities n1, n2 and n3 respectively, we must provide clauses defining the connective predicates "and_label1/(n1+1)", "or_label2/(n2+1)" and "agr_label3/(n3+1)", where the extra argument of each predicate is intended to contain the result achieved after the evaluation of the proper connective. For instance, in the boolean case, the following two facts model in a very easy way the behaviour of the classical conjunction operation: and_bool(0,X,0). And_bool(1,X,X).

member(X) :- number(X),0=<X,X=<1.
bot(0). top(1).
leq(X,Y) :- X=<Y.
and_luka(X,Y,Z) :- pri_add(X,Y,U1),pri_sub(U1,1,U2),pri_max(0,U2,Z).
and_godel(X,Y,Z):- pri_min(X,Y,Z).
and_prod(X,Y,Z) :- pri_prod(X,Y,Z).

or_luka(X,Y,Z) :- pri_add(X,Y,U1),pri_min(U1,1,Z).

or_godel(X,Y,Z) :- pri_max(X,Y,Z).
or_prod(X,Y,Z) :-pri_prod(X,Y,U1),pri_add(X,Y,U2),pri_sub(U2,U1,Z).
agr_aver(X,Y,Z) :- pri_add(X,Y,U),pri_div(U,2,Z).
pri_add(X,Y,Z) :- Z is X+Y. pri_min(X,Y,Z) :- (X=Y,Z=Y).
pri_sub(X,Y,Z) :- Z is X-Y. pri_max(X,Y,Z) :- (X=Y,Z=X).
pri_prod(X,Y,Z) :- Z is X * Y. pri_div(X,Y,Z) :- Z is X/Y.

Figure 1: [0,1] lattice (download)

The reader can easily check that the use of lattice "bool.pl" when working with MALP programs whose rules have the form "A ←_bool &_bool(B₁, ... ,B_n) with 1", being A and B_i typical atoms, successfully mimics the behaviour of classical Prolog programs where clauses accomplish with the shape "A : - B₁, . . . ,B_n". As a novelty in the fuzzy setting, when evaluating goals each output will contain the corresponding Prolog's substitution (i.e., the crisp notion of computed answer obtained by means of classical SLD-resolution) together with the maximum truth degree 1. On the other hand, in Figure 1 we have modeled the more flexible lattice (that we will mainly use in our examples, beyond the boolean case) which enables the possibility of working with truth degrees in the infinite space of the real numbers between 0 and 1, allowing too the possibility of using conjunction and disjunction operators recasted from the three typical fuzzy logics described before (i.e., the Lukasiewicz, Gödel and product logics), as well as an useful description for the hybrid aggregator average. Note also we have included definitions for auxiliary predicates, whose names always begin with the prefix "pri ". All them are intended to describe primitive/arithmetic operators (in our case +, -, *, /, min and max) in a Prolog style, for being appropriately called from the bodies of clauses defining predicates with higher levels of expressivity (this is the case for instance, of the three kinds of fuzzy connectives we are considering: conjuntions, disjunctions and agreggations).

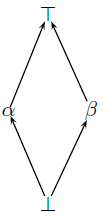
Since till now we have considered two classical, fully ordered lattices (with a finite and infinite number of elements, collected in files "bool.pl" and "num.pl", respectively), we wish now to introduce a different case coping with a very simple lattice where not always any pair of truth degrees are comparable. So, consider the following partially ordered multi-adjoint lattice in the diagram below for which the conjunction and implication connectives based on the Gödel intuistionistic logic conform an adjoint pair.... but with the particularity now that, in the general case, the Gödel's conjunction must be expressed as &G(x, y) ≜ inf(x, y), where it is important to note that we must replace the use of "min" by "inf" in the connective definition.

member(bottom).
member(alpha).
member(beta).
member(top).
members([bottom,alpha,beta,top]).
leq(bottom,X). leq(X,top).
leq(X,X).
and_godel(X,Y,Z) :- pri_inf(X,Y,Z).
pri_inf(bottom,X,bottom):-!.
pri_inf(alpha,X,alpha):-leq(alpha,X),!.
pri_inf(beta,X,beta):-leq(beta,X),!.
pri_inf(top,X,X):-!.
pri_inf(X,Y,bot).

Figure 2: Example of lattice (download)

To this end, observe in the Prolog code accompanying the figure above that we have introduced five clauses defining the new primitive operator "pri_inf/3" which is intended to return the infimum of two elements. Related with this fact, we must to point out the following aspects:

• Note that since truth degrees α and β (or their corresponding representations as Prolog terms "alpha" and "beta" used for instance in the definition(s) of "member(s)/1") are incomparable then, any call to both "?- leq(alpha,beta)." or "?- leq(beta,alpha)." will always fail.
• Fortunately, a goal of the form "?- pri_inf(alpha,beta,X).", or alternatively "?- pri_inf(beta,alpha,X).", instead of failing, successfully produces the desired result "X=bottom".
• Note anyway that the implementation of the "pri_inf/1" predicate is mandatory for coding the general definition of "and_godel/3".

In order to test the capability of FLOPER for handling lattices, we have prepared these examples:

• num: Reals from 0 to 1
• nat: Naturals form 0 to 10 divided by 10
• bool: Booleans
• bool × bool: Booleans²
• num × {a,b,c,d}: A cartesian product of lattices
• {bottom,alpha,beta,top}: The example lattice from figure 2
• info([0,1],[0,inf]): Reals from 0 to 1 with weights form 0 to inf