Every MALP program has a Multi-Adjoint Lattice associated. This lattice defines the concept of Truth (as truth degrees) and how atoms can be connected in the body of the rules (connectives).

In VisualFLOPER, each Project has one, and only one associated lattice (as the concepts of Truth and connectives have to be the same for all fuzzy programs of the Project). This Lattice is defined as a .lat file, which is a pure Prolog file containing some predicates (see section Multi-Adjoint Lattices in this web).

The user is not allowed to remove the lattice file, nor include more of them. But it is possible to edit the lattice, or replace it with another one using File > Replace Lattice File in Project.

The default lattice corresponds to [0,1] interval (num.lat file), which includes the connectives given by Lukasiewicz, Gödel and Product logics.

Through Show option VisualFLOPER (and FLOPER) lists the content of the loaded lattice. For instance, is the loaded latice were num.lat ([0,1] interval), Show option would list the following lines:

:- dynamic and_prod/3, and_godel/3, and_luka/3, or_prod/3, or_godel/3, or_luka/3, agr_aver/3, pri_prod/3, pri_div/3, pri_sub/3, pri_add/3, pri_min/3, pri_max/3.

 

member(X):-number(X), 0=<X,X=<1.

 

leq(X,Y):-X =< Y.

 

bot(0).

top(1).

 

and_prod(X,Y,Z) :- pri_prod(X,Y,Z).

and_godel(X,Y,Z) :- pri_min(X,Y,Z).

and_luka(X,Y,Z) :- pri_add(X,Y,U1), pri_sub(U1,1,U2), pri_max(U2,0,Z).

 

or_prod(X,Y,Z) :- pri_prod(X,Y,U1), pri_add(X,Y,U2), pri_sub(U2,U1,Z).

or_godel(X,Y,Z) :- pri_max(X,Y,Z).

or_luka(X,Y,Z) :- pri_add(X,Y,U1), pri_min(U1,1,Z).

 

agr_aver(X,Y,Z)   :- pri_add(X,Y,U1),pri_prod(U1,0.5,Z).

agr_aver2(X,Y,Z) :- or_godel(X,Y,U01), or_luka(X,Y,U02),

                            pri_add(U01,U02,U1),pri_div(U1,2,Z).

 

pri_prod(X,Y,Z) :- Z is X * Y.

pri_div(X,Y,Z) :- Z is X / Y.

pri_sub(X,Y,Z) :- Z is X-Y.

pri_add(X,Y,Z) :- Z is X+Y.

pri_min(X,Y,Z) :- (X=<Y,Z=X;X>Y,Z=Y).

pri_max(X,Y,Z) :- (X=<Y,Z=Y;X>Y,Z=X). % max(x,y) 

FLOPER, as VisualFLOPER, allows only one lattice. Use option lat and write the path to the new lattice to load one. This option checks the existence of the main elements of .lat files:

1. member/1
2. top/1
3. bot/1
4. leq/2
5. members/1

Figure 1 shows the screenshot of the use of this option.

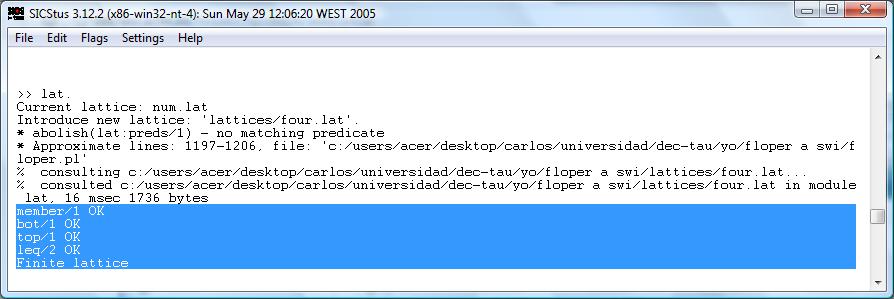
Figure 1: Loading a lattice